静态链表

right为链表每个元素的后继下标；

双向静态链表

双向链表，有前驱有后继。

8的后继为0，表示这是一个循环链表

56 9 12 23 49 20 16 62

0 > 1 >2>3> 4 >5 >6 >7 > 8 > 0

树

n个节点可以构成不相似的二叉树的数量有：

b_n表示n个结点构成的不同形态的二叉树的数量。
$$
b_n=
\begin{cases}
b_0=1\
b_n=\sum_{i=0}^{n-1}b_ib_{n-i-1}
\end{cases}
$$
结论：
$$
b_n = \frac{1}{n+1}·C^n_{2n}
$$

图

vertex n.顶点

重连通图

即，任意两个顶点之间含有不止一条通路，这个图就称为重连通图；

关节点：如果删除某个顶点及其相关联的边后，原来的图被分割为两个及以上的联通分量，则称该顶点为无向图的一个关节点。

判断一个重连通图

判断图中是否有关节点，没有则表示图为重连通图。

拓扑算法

n: 拓扑序列

拓扑排序：从某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

Dijkstra算法

带权单源最短路径算法。

图来源：https://blog.csdn.net/xiaoxi_hahaha/article/details/110257368

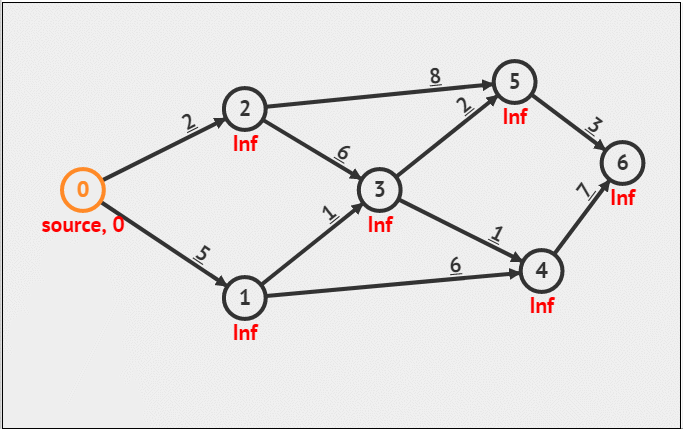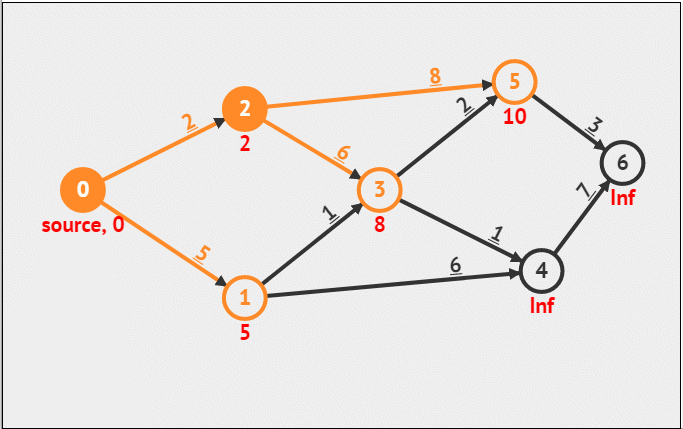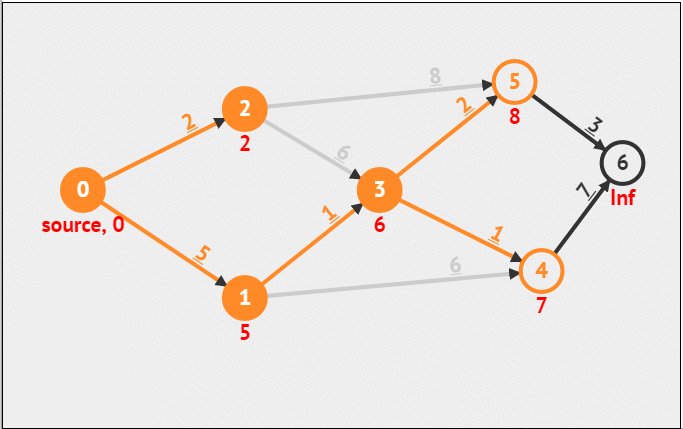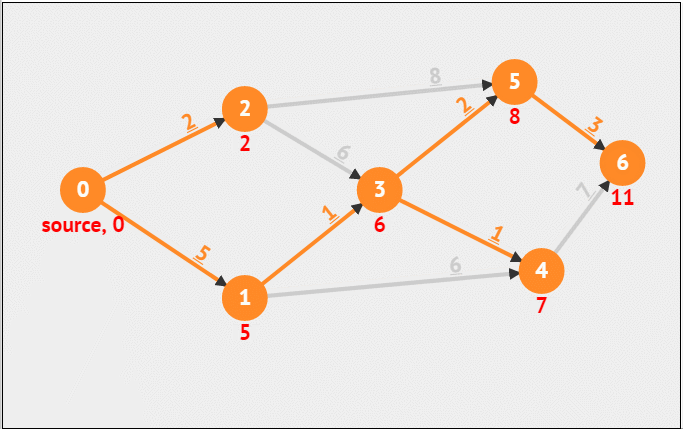
Floyd算法

带权最短路径

查找表

静态查找表和动态查找表

静态查找表：只进行查找操作，不改动表中数据元素；

动态查找表：在查找的同时进行数据的增加和删除操作。

关键字

表中元素的属性，可以作为关键字。比如学生有姓名、学号、年龄等属性，这些都可以作为关键字。

主关键字和次关键字

主关键字：唯一标识一个数据元素，比如学号；

次关键字：与主关键字相反，如姓名、年龄。

一些名词

静态查找树
- 次优查找树
- 二叉排序树

哈希表

http://c.biancheng.net/view/3437.html

哈希函数

直接定值法：H(key) = key 或 H(key) = a * key + b
数字分析法：取出每个值中不同部分较多的地方作为哈希地址；
平方取中法：对关键字进行平方操作，取中间几位作为哈希地址；
折叠法：将关键字分为几个部分，然后取这几部分的叠加和作为哈希地址；
除留余数法：若已知哈希表长度m，取一个不大于m的数字p，然后对关键字进行取余运算
- H(key) = key % p
随机数法：取关键字的一个随机函数值作为哈希地址，即H(key) = random(key);

选择一个哈希函数

需要注意的地方：

若关键字长度不等，可以用随机数法；
关键字位数多，折叠法或数字分析法；
关键字位数较短，平方取中法；
哈希表大小已知，可以选择除留余数法；
关键字分布情况；
查找表的查找频率；
计算哈希函数需要的时间；

处理冲突

开放定址法：H(key) = [ H(key) + d ] MOD m;
- $$
  H(key) = [ H(key) + d ]\ %\ m
  $$
- m为哈希表表长
- d的取值
  - 线性探测法：d = 1,2,3, …, m-1
  - 二次探测法：d=12, -12, 22 , -22, 32 …
  - 伪随机数探测法：d=伪随机数
再哈希法：
- 若发生冲突，再使用另一个哈希函数进行计算，直到冲突不再发生；
链地址法
- 将处于一个地址的值放在一个链表中；
建立一个公共溢出区
- 建立两张表，一张基本表，一张溢出表；
- 将哈希函数结果产生冲突，就将数据放到公共溢出区；

B-树 (B-Tree)

名字

这里不是B减树，B-树，指的就是B树。换言之，B树，就是B-树。

B+树是B树的plus，不存在B减树；

满足下列要求的m叉树

树中每个结点至多有m个孩子结点（即，至多有m-1个关键字）
每个结点的结构如下：

\

\
除根节点外，其他结点至少有⌈m/2⌉个孩子结点；
若根节点不是叶子节点，则根节点至少有两个孩子结点，（即根节点没有只有一个孩子结点的情况）；
所有的叶子节点都在同一层上，即B树是所有节点平衡因子均等于0的多路查找树。
除根节点外，其他结点都包含n个key，这里⌈m/2⌉-1 <= n <= m-1
$$
\lceil m/2 \rceil - 1 \leq n \leq m-1
$$